Albert Einstein is widely reported as having made the statement, “The most powerful force in the universe is compound interest,” and after looking at the math behind this concept, I definitely agree with him.
Definition
Wikipedia defined the concept of compound interest as elegantly as I’ve seen: “Compound interest arises when interest is added to the principal of a deposit or loan, so that, from that moment on, the interest that has been added also earns interest. This addition of interest to the principal is called compounding.”
I know a lot of people can get lost with detailed mathematical formulas, so we’ll skip those, but this is so unbelievably important to understand and appreciate that we need to run an example.
An Example
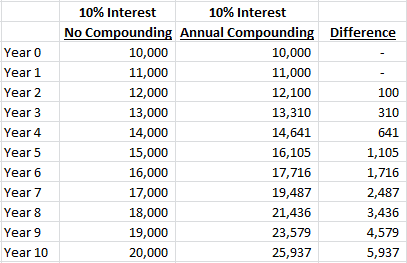
Let’s say you deposit $10,000 into an account that pays 10% interest and it compounds once annually. At the end of the first year you have your original $10,000 plus the $1,000 interest you earned ($10,000 x 10% = $1,000) for a total of $11,000.
At the end of the second year you’ve earned $1,100 in interest ($11,000 x 10% = $1,100), which is added to your $11,000 balance for a total of $12,100.
If compounding didn’t exist and you were only paid the 10% interest on your initial deposit, you’d have a total of $12,000 (your original $10,000 plus $1,000 interest paid at the end of Year 1 and another $1,000 paid at the end of Year 2).
This $100 difference doesn’t sound like much, right? How can this be “the most powerful force in the universe” or a “miracle” as it is often called?
Let’s look at this example at different intervals over a 100-year period:
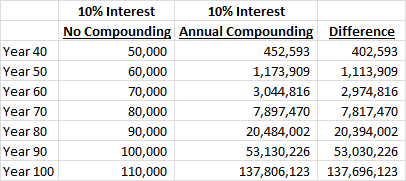
Just for fun though, first try to guess how much the final balance will be in the compounded example at the end of Year 100 and let me know what your guess was in the comments section below (as a little inspiration, you know the non-compounded number will be $110,000 (100 years of $1,000 interest pus $10,000 initial investment)):
At the end of Year 10 we’re up to a $5,937 difference, which is a large number, but still not life-changing.
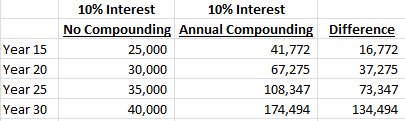
By Year 25 we’re already almost up to the full $110,000 you would have in the ‘no compounding’ example at Year 100.
At the end of Year 30 the difference has ballooned to $134,494. The ‘no compounding’ example has $40,000 as you would expect (30 years of $1,000 interest plus the original $10,000), but the compounded version has $174,494!
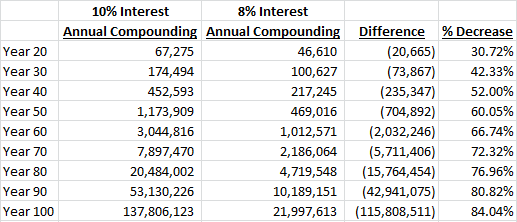
By the end of Year 50 the difference is up to $1,113,909 and amazingly by the end of Year 100 the compound interest example has a balance of $137,806,123 compared to only $110,000 in the non-compounded version. Yes, that is $137.8 MILLION dollars! It’s not a typo or a joke — that’s just the math.
Now you can see why everyone who understands this concept is so blown away by it!
The most important take away from this example is that compounding matters and the length of time matters, so you need to allow this miracle of compounding as much time as possible to work its magic. Invest as early in life as you possibly can with as much money as you possibly can!
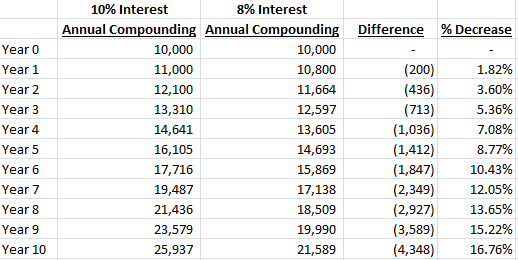
Let’s look at the compounding example but with “only” an 8% interest rate:
Again, the difference isn’t that large after Year 10, but let’s look out to Year 100:
While the difference between the 10% and 8% rates doesn’t sound enormous in theory, you would have $115,808,510 less at the end of Year 100 in the 8% example (or only 15.96% of the total balance)!
What that means to me is that every little bit of additional return on your investment is essential, and you have to do everything in your power to maximize your return.
As we’ll show in a follow up post, since there basically isn’t a person alive who can beat the stock market returns over a 50 or 100 year period, the best way possible to do this is to invest in an ultra-low expense ratio mutual fund that mirrors the total U.S. stock market.
Richmond Savers has partnered with CardRatings for our coverage of credit card products. Richmond Savers and CardRatings may receive a commission from card issuers.